We (can) consider 4/4 time as "basic material" and all other times as "transformations", where deletion of certain beats is the essential mechanism of transformation. So we get 7/8, 6/8, 3/4, 5/8 …
     Why not (possible to) consider each of the above times as a "whole", writing e.g. 7/8 as 7/7, or 5/8 as 5/5 and so on? In simple words: Why not writing a waltz in 3/3 or 6/6?
     I have a vague understanding of the matter, but would be glad if you can tell the reason in one or two sentences. A short and stupid answer would be: we need 1/5, 1/7, 1/3, 1/6 notes. I guess these notes we could have if needed. So this isn't the right short answer, isn't it? Writing this I am increasingly thinking this is a silly question, nevertheless I'll post it.
     P.S. What about 9/8 I think I have seen?

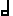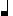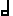     Using our habitual,,,durations, let's start from the end and observe what an abomination a complete bar of 9/8 looks like: a dottedtied to a dotte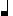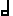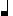d, (._.). This is the price to be paid for the binary-based system which we presently use. Yours is not a silly question and we hope that our answer will not be stupid.
     Because our answer is very much what you suspected, that we would need values of 1/3 and 1/9, not to mention 1/5 and 1/7 for more complex situations. Creating, naming, and symbolizing these new values would be more trouble and cause more confusion than the result would justify.
     Musical rhythm being fundamentally and habitually binary, the binary system which we presently use, verbally and graphically, seems to be the best solution.
     As you probably have noticed by now, what we would really like to change is a lot more of the existing terminology, but we really do not dare because the few changes already suggested have drawn an appreciable amount of flack. Thanks for your letter, it was fun for us.